Par Kai Kaufhold
Aperçu global
En 2020, l’ICA a mis sur pied un groupe de surveillance de projet (GSP) chargé de commander une recherche sur l’amélioration de la mortalité au Canada qui pourrait servir de base à une nouvelle échelle de projection de la mortalité utilisée dans tous les domaines de la pratique actuarielle. Dans sa demande de propositions, le GSP a souligné que la recherche devrait tenir compte des pratiques exemplaires à l’échelle internationale et comprendre un examen des méthodes et des modèles existants de projection de la mortalité. En outre, le GSP a demandé aux chercheurs d’envisager un cadre général pour mettre à jour périodiquement les hypothèses d’amélioration de la mortalité.
Ayant acquis plus d’une décennie d’expérience en modélisation de la longévité sur les marchés du transfert de risques liés aux régimes de retraite au Royaume‑Uni et au Canada, la société d’expertise‑conseil Ad Res s’est associée à des chercheurs de l’Université des sciences appliquées de Coblence qui venaient de terminer un projet de recherche comparant une vaste gamme de modèles de mortalité. Nous avons lancé le projet de recherche au début de 2021 et nous avons travaillé en étroite collaboration avec le GSP pendant toute la durée du projet, du printemps 2021 à l’automne 2023.
Quelles constatations clés les actuaires peuvent‑ils tirer du rapport de recherche publié en avril 2024?
- Les taux d’amélioration de la mortalité (AM) sont très volatils, ce qui nécessite des modèles statistiques pour analyser les résultats de mortalité observés. Les données sur la mortalité de la population canadienne montrent des tendances claires selon l’âge, la période et la cohorte d’après l’année de naissance, qui doivent toutes être prises en compte lors de la projection des taux de mortalité futurs.
- L’équipe de recherche et le GSP ont sélectionné le modèle statistique le plus approprié à partir d’une liste exhaustive de modèles candidats établie en fonction de la qualité de l’ajustement et de la robustesse, ce qui signifie que le modèle sélectionné saisit les principales caractéristiques des tendances de mortalité observées dans les données canadiennes et que les résultats ne devraient pas être sensibles à la modification de la fourchette de données, ou à d’autres choix de modèle.
- L’équipe de recherche a élaboré un cadre de modèle fondé sur le modèle CMI[1], qui nous permet de concilier les résultats d’un modèle stochastique de mortalité avec un taux déterministe d’AM à long terme en produisant des résultats cohérents.
- L’étalonnage du modèle stochastique de mortalité selon l’âge, la période et la cohorte portant sur les données démographiques canadiennes de 1980 à 2019 permet d’obtenir un taux d’AM unisexe moyen à long terme de 1,3 % par année pour les 40 à 90 ans, à partir de 2050.
- En contrôlant des effets de période et de cohorte, la période d’observation de 40 ans offre le taux le plus faible d’AM à long terme. Des plages de données plus courtes et plus longues entraîneraient des taux moyens plus élevés.
Processus de recherche
Le projet de recherche de l’ICA sur l’amélioration de la mortalité comportait plusieurs objectifs clés qui sont résumés dans le rapport publié :
- Examen approfondi de la documentation
- Examen des sources de données disponibles
- Mise en œuvre de modèles de mortalité présélectionnés
- Élaboration d’un cadre de projection déterministe de la mortalité tel que la méthode CMI
- Analyses de scénarios
Pour chaque objectif de recherche, l’équipe de recherche et le GSP ont tenu plusieurs réunions pour présenter les résultats préliminaires, en vue d’une discussion plus approfondie et de la confirmation des divers produits livrables.
Examen de la documentation
L’analyse documentaire a porté sur une vaste liste de publications universitaires et sur des documents de travail et des publications de recherche provenant d’autres organismes actuariels, comme la Society of Actuaries (SOA) et l’Institute and Faculty of Actuaries (IFoA). L’exercice visait principalement à obtenir un aperçu de l’ensemble des connaissances actuelles et à déterminer la portée de nos enquêtes. Les modèles et les méthodologies que nous avons décidé d’exclure renfermaient entre autres choses des modèles de mortalité à plusieurs populations qui projettent simultanément et de manière cohérente les tendances pour différentes sous‑populations. Cette classification de modèles est importante lorsqu’on tente de comprendre les différences entre les tendances de mortalité pour divers groupes socioéconomiques. De même, l’analyse de la contribution des différentes causes de décès aux tendances de la mortalité a été reportée à des travaux de recherche futurs. De même, nous avons décidé de ne pas mettre en œuvre des modèles bayésiens de projection de la mortalité qui peuvent exiger beaucoup de ressources. Ces modèles seraient intéressants pour un projet de suivi portant sur les marges de risque et l’incertitude des taux d’AM.
Sources de données
Parmi les sources de données, nous avions le choix entre les données du Régime de pensions du Canada et du Régime de rentes du Québec, les données de la Sécurité de la vieillesse, les données sur l’assurance vie recueillies par l’ICA et les données sur la population. Nous avons sélectionné les données sur la population canadienne publiées par le projet Human Mortality Database (HMD), car elles fournissent l’ensemble de données le plus cohérent sur toute la tranche d’âge et sur une longue période historique (1921 à 2019 à l’époque).
Mise en œuvre de modèles
Après notre analyse documentaire, nous avons conservé une liste restreinte de 14 modèles de mortalité, couvrant des modèles stochastiques pour les taux de mortalité et les taux d’amélioration de la mortalité, à partir de la catégorie des modèles généralisés fondés sur l’âge, la période et la cohorte. Le modèle le plus simple de ce genre, le modèle appelé « APC » ou modèle âge-période-cohorte, et le modèle intégré âge-période-cohorte ou « APCI », se sont révélés être les modèles les plus robustes qui saisissaient toutes les tendances des caractéristiques des données. La principale différence entre ces deux modèles est que le modèle APCI décrit explicitement la composante âge des améliorations de la mortalité comme un processus temporel linéaire, tandis que le modèle APC permet à l’utilisateur de choisir librement le processus de série chronologique pour projeter les taux de mortalité futurs. Par ailleurs, le modèle APC sous‑entend que les taux de mortalité s’améliorent uniformément à tous les âges, une fois soustraite la composante de cohorte. En résumé, les deux modèles que nous avons jugés adéquats permettent de solides hypothèses simplificatrices. Rappelez‑vous que les modèles représentent toujours un compromis entre la simplicité et la qualité de l’ajustement, d’où l’importance de tester divers modèles.
Établissement du taux d’AM à long terme
Outre les modèles stochastiques de mortalité, qui sont les plus courants dans les études universitaires, les praticiens et praticiennes en actuariat à l’échelle internationale utilisent également des modèles de projection déterministes. Parmi les principaux exemples, citons la SOA, dont le Longevity and Mortality Strategic Research Program a publié un modèle d’amélioration de la mortalité (MAM) fondé sur les données historiques de l’United States Social Security Administration, et la Continuous Mortality Investigation de l’IFoA, qui a publié une série de modèles de projection, appelés modèles CMI. Dans nos travaux, nous avons utilisé une variante du modèle CMI pour décomposer les tendances récentes en matière d’amélioration de la mortalité en composantes d’âge, de période et de cohorte, à l’aide du modèle APCI, qui se prête particulièrement bien à cette tâche. Chacune des composantes est ensuite projetée dans l’avenir. Voici nos principales hypothèses :
- Les effets de période représentent des fluctuations temporaires autour de la tendance linéaire implicite du modèle APCI, de sorte qu’ils peuvent être bien modélisés à l’aide d’une marche aléatoire.
- Les effets de cohorte sont également mieux modélisés à l’aide d’un processus stationnaire sans contribution d’AM à long terme à partir de la composante cohorte.
Autrement dit, nous avons fixé à zéro les taux d’AM à long terme pour les composantes période et cohorte, ce qui laisse la composante âge comme seul élément contributeur aux taux d’AM à long terme. Après une période de convergence de 30 ans, nous supposons un seul taux d’AM, qui est indépendant de l’âge.
Remarque : les figures suivantes sont disponibles en anglais seulement.
Figure 1 : Illustration des taux d’AM stochastiques et déterministes
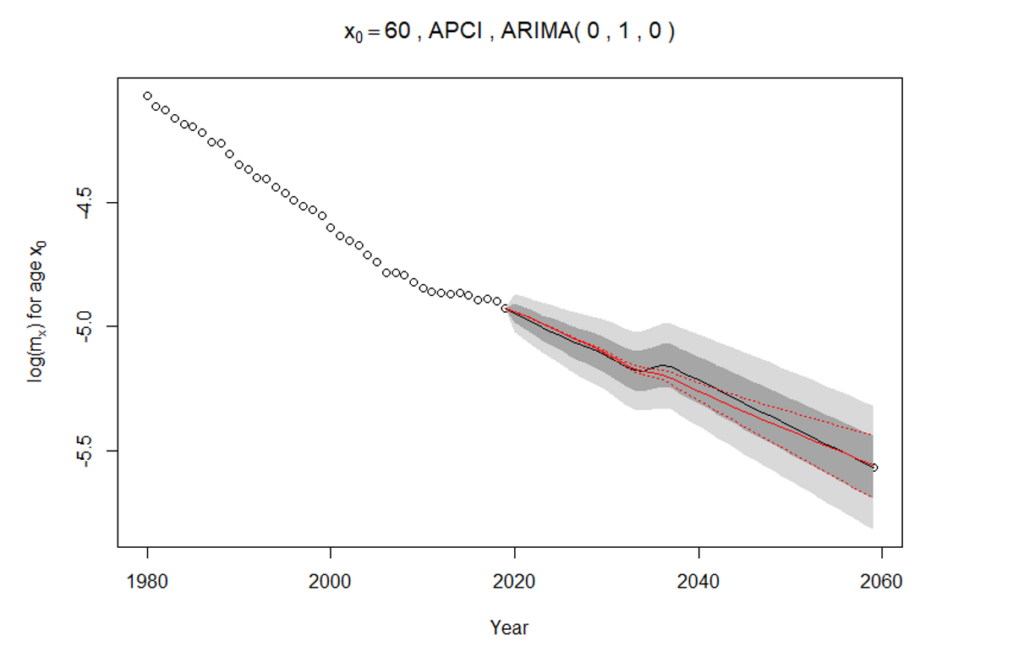
Plutôt que de choisir subjectivement un taux à l’aide des commentaires d’experts, nous déterminons le taux d’AM à long terme qui correspondrait au résultat médian de notre prévision stochastique de la mortalité à partir du modèle de projection APCI ou du modèle de projection APC. Cela est illustré à la figure 1, qui montre les taux de mortalité historiques et futurs des hommes âgés de 60 ans sur une échelle logarithmique. Les cercles représentent les taux de mortalité logarithmique de 1980 à 2019. Les zones grises représentent les intervalles de confiance pour les prévisions stochastiques de mortalité, la prévision médiane correspondant à une ligne noire continue. La ligne rouge continue représente la projection déterministe de l’AM, obtenue en minimisant les erreurs quadratiques entre la projection déterministe et la prévision stochastique médiane.
La figure 2 montre les taux d’amélioration de la mortalité normalisés selon l’âge, à la fois historiques (cercles rouges) et modélisés (ligne continue). La projection déterministe selon le modèle CMI est illustrée par la ligne pointillée, indiquant à la fois le point de départ inférieur, par rapport au taux d’AM de 2019, et la convergence progressive vers un taux à long terme sur 30 ans. Il convient de noter que dans la mise en œuvre finale de la projection du modèle CMI pour la meilleure estimation proposée, nous avons éliminé l’augmentation apparente des taux d’AM projetés entre 2020 et 2030. Veuillez consulter le rapport pour plus de détails.
Figure 2 : Taux normalisés d’amélioration de la mortalité – Hommes
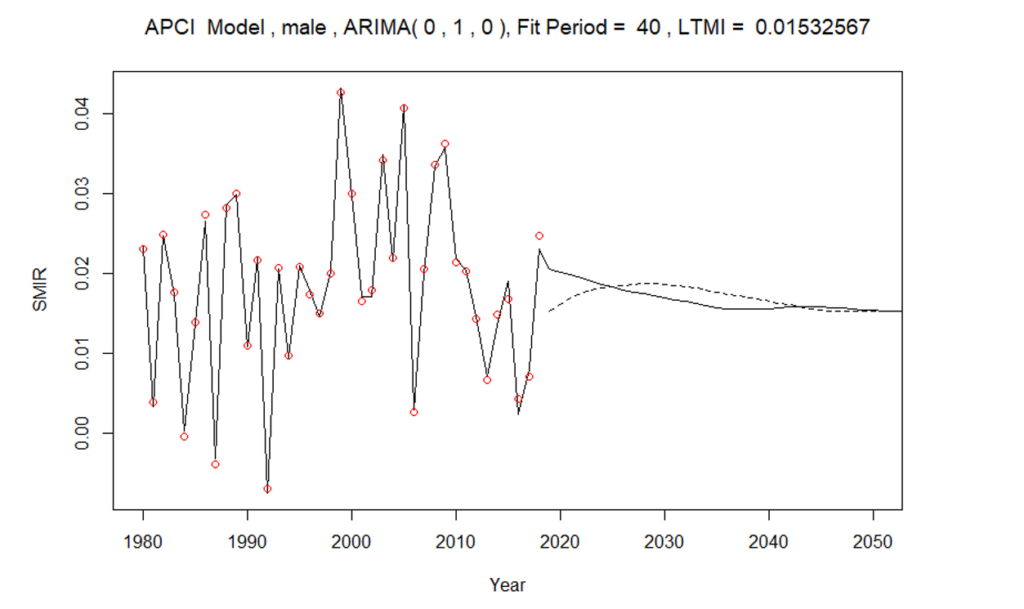
Pour le modèle APCI, le taux d’AM équivalent à long terme se situe entre 1,4 % et 1,5 %, en prenant la moyenne des taux d’AM des hommes et des femmes. Comme il a été mentionné précédemment, le modèle APCI sous‑entend une tendance linéaire de l’AM pour la composante d’âge. Lorsque nous choisissons la marche aléatoire avec dérive pour le modèle APC, notre modèle de candidat finaliste, nous obtenons le même résultat. Autrement dit, le terme « dérive » dans la marche aléatoire donne le même résultat que l’hypothèse linéaire de l’APCI. Toutefois, si nous choisissons un processus de séries chronologiques d’ordre plus élevé, le modèle ARIMA(1,2,1), le taux d’AM à long terme pour les hommes s’avère inférieur à celui des femmes, qui était de 1,3 %. C’est pourquoi les taux d’AM à long terme que nous recommandons, fondés sur la meilleure estimation et appliqués selon la méthode CMI adaptée décrite dans notre rapport, sont de 1,3 %.
Compte tenu à la fois de l’incertitude stochastique et de l’erreur d’estimation, nous constatons que la fourchette raisonnable dans laquelle un taux d’AM unisexe à long terme devrait se situer est de 1,0 % à 1,9 %, pour les âges compris entre 40 à 90 ans applicables à compter de 2050.
Analyses de scénarios
L’échelle de projection fondée sur la meilleure estimation, que nous avons soumise au GSP à la fin de 2022, a depuis fait l’objet d’essais exhaustifs. Pour chaque choix de modèle effectué en cours de route, nous avons tenu compte des hypothèses qui auraient pu constituer des hypothèses de rechange raisonnables et nous en avons testé l’incidence. Cela nous donne une grande confiance que notre meilleure estimation est robuste.
Le choix ayant la plus grande incidence sur le résultat final est naturellement le choix de la plage de données; c’est pourquoi nous avons testé tous les autres choix possibles de période d’étude. Les détails de ces tests se trouvent dans le rapport, mais le résultat le plus frappant a été que la période d’observation de 40 ans que nous avions choisie parce qu’elle offrait un bon équilibre entre les données récentes les plus pertinentes et une période historique suffisamment longue pour pouvoir extrapoler avec confiance dans l’avenir, offre les taux d’AM moyens à long terme les plus faibles parmi tous les choix raisonnables.
Autre constatation importante : le choix du lissage a un impact marquant sur le résultat global. Pour cette raison, nous avons pris soin de recourir le moins possible au lissage et de nous assurer de conserver les caractéristiques des résultats non lissés. Selon une hypothèse importante qu’il convient de mentionner, les paramètres du modèle décrivant les effets de période ne devraient pas être lissés, car nous devons nous attendre à ce que la mortalité varie d’une année civile à l’autre. En revanche, les âges et les cohortes voisins devraient afficher des transitions harmonieuses des taux de mortalité et aucun saut. Par conséquent, nous appliquons une approche de log‑vraisemblance pénalisée pour générer des estimations lisses pour les paramètres d’âge et de cohorte.
L’équipe de recherche a également examiné l’incidence potentielle de la COVID‑19 sur les tendances de mortalité de la population canadienne en désagrégeant les données hebdomadaires groupées par tranche d’âge sur les fluctuations de la mortalité à court terme fournies par la HMD en décès par âges individuels. Notre examen confirme les nouvelles constatations de la recherche selon lesquelles l’utilisation des années civiles 2020 ou 2021 comme point de départ pour la projection des séries chronologiques entraînerait des distorsions qui ne refléteraient probablement pas la véritable tendance sous‑jacente de la mortalité à long terme. Les recherches publiées en 2021 et 2022 montrent que même si la tendance sous‑jacente devrait généralement être stable, l’occurrence d’une pandémie rehausse le niveau d’incertitude lié aux projections de mortalité.
Conclusion et perspectives
Le principal résultat de notre recherche sur les tendances de la mortalité au Canada est un cadre visant à établir des hypothèses de tendance de la mortalité qui peuvent être facilement appliquées aux données émergentes. En modélisant la mortalité toutes causes confondues chez les hommes et les femmes au Canada âgés de 40 à 90 ans, nous avons examiné un large éventail de modèles candidats comportant des composantes d’âge, de période et de cohorte. Les modèles qui conviennent le mieux selon la qualité de l’ajustement et la robustesse, compte tenu des données, étaient les modèles APCI et APC. Les prévisions stochastiques résultant de ces modèles peuvent être rapprochées à un taux déterministe d’AM à long terme dans le style du modèle CMI, en trouvant le taux à long terme qui, pour la tranche d’âge modélisée, donne l’erreur quadratique moyenne la moins élevée.
Les principales limites de la recherche ont porté sur le fait que nous n’avons pas modélisé des tendances distinctes pour différentes causes de décès, et notre approche unique de modélisation de la population ne reflète pas différents groupes socioéconomiques qui peuvent connaître des tendances de mortalité différentes. De plus, à mesure que d’autres données émergeront après la pandémie de COVID‑19, il sera logique d’élargir le cadre de modélisation pour permettre explicitement les sauts de mortalité.
Nous encourageons tous les praticiens et praticiennes dont les travaux comprennent l’application de projections de mortalité à tester les taux fondés sur la meilleure estimation proposés avec le rapport publié. Une analyse détaillée des répercussions ne s’appliquait pas au projet de recherche, mais les groupes de parties prenantes de l’ICA sont à l’œuvre pour formuler des recommandations.
En 2011, Kai Kaufhold a créé la société d’expertise-conseil en actuariat Ad Res. Fort de plus de 25 ans d’expérience dans le secteur de la réassurance vie et santé, il fournit des services de conseil aux réassureurs, aux sociétés d’assurance vie et aux administrateurs de régimes de retraite. Ses consultations couvrent un large éventail de sujets, notamment le risque de longévité, la tarification de la réassurance, les hypothèses relatives à l’amélioration de la mortalité et la stratégie de réassurance. Pour toute question ou commentaire, vous pouvez communiquer avec lui à l’adresse kai.kaufhold@adreservices.com.
Cet article présente l’opinion de son auteur et ne constitue pas un énoncé officiel de l’ICA.
[1] Nommé d’après l’enquête continue sur la mortalité (Continuous Mortality Investigation) menée par l’Institute and Faculty of Actuaries du Royaume‑Uni.


