Alert Test

This banner is a test to see if it works. Thank you.

The cia
Retour aux Actualités

Simplicité, interprétabilité et sélection efficace des variables grâce à la régression LASSO

Articles Science des données

Par David Hatherell et Louis Rossouw

Ces dernières années, les champs de l’apprentissage automatique, de l’apprentissage profond et de l’analytique avancée ont révolutionné plusieurs domaines, notamment la modélisation de la mortalité. Ces technologies dernier cri présentent des avantages concrets, car elles améliorent la précision, l’interprétabilité et l’efficacité des modèles prédictifs.

Dans cet article, nous étudions les concepts clés d’une technique de ce genre – la régression LASSO (Least Absolute Shrinkage and Selection Operator) – et examinons ses avantages distinctifs. Par ailleurs, nous montrons comment la régression LASSO se démarque en tant que technique puissante permettant de contourner les difficultés courantes qu’entraîne l’existence de plusieurs variables prédictives.

Comprendre la régression LASSO

La régression LASSO s’appuie sur les principes de la régression linéaire généralisée, tout en introduisant un terme de régularisation qui améliore la performance du modèle. La technique cherche à minimiser la formule suivante :

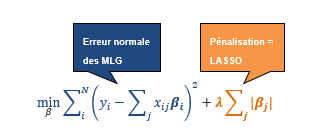
Formule d'équation

où :

  • yⅈ représente la variable de réponse de la ie observation.
  • χⅈj représente la je valeur de la variable indépendante de la ie observation.
  • βj représente le coefficient de régression associé à la je valeur de la variable indépendante.
  • λ représente le terme de régularisation.

Dans les modèles linéaires généralisés (MLG), nous estimons les coefficients suivant la méthode des moindres carrés ordinaires (MMCO). La technique LASSO ajoute un terme de pénalité à l’équation de la MMCO afin de minimiser l’erreur. La pénalité totale appliquée correspond à la somme des valeurs absolues des coefficients, multipliée par un certain lambda. Si le lambda a une valeur nulle, nous obtenons l’équation de la MMCO qui comprend toutes les variables de la formule des modèles.

L’augmentation des coefficients fait tendre lambda vers zéro et entraîne la mise à zéro de certains de ces coefficients (supprimant de fait la variable du modèle). De cette façon, le modèle LASSO détermine quelles variables ont une influence sur le résultat réel en se fondant sur les données fournies.

Validation croisée

La validation croisée est couramment utilisée par diverses techniques d’apprentissage automatique pour évaluer et établir des hyperparamètres sans utiliser de données réservées ou données de test distinctes. Cela vise à réduire le risque de surajustement des données. La validation croisée suit les étapes suivantes :

  1. Diviser les données d’entraînement en plusieurs blocs (disons cinq).
  2. Ajuster un modèle à quatre blocs de données et effectuer la validation au moyen du cinquième.
  3. Répéter le processus jusqu’à ce que chaque bloc ait été utilisé.
  4. Calculer la moyenne du terme d’erreur sur la totalité des blocs.

Dans le cas de la régression LASSO avec validation croisée, cette dernière sert à définir les paramètres lambda. Il en résulte des modèles qui dépendent du niveau et de la cohérence des relations entre les données. Par conséquent, ces modèles sont moins enclins au surajustement.

Trois avantages de la régression LASSO avec validation croisée

Sélection de variables

En intégrant un terme de pénalisation, la régression LASSO optimise conjointement deux aspects critiques :

  1. Qualité de l’ajustement : à l’instar des MLG, la régression LASSO vise l’obtention d’un bon ajustement aux données.
  2. Structure des coefficients : la régression LASSO cherche une structure souhaitable pour les coefficients estimés.

La pénalité incite certains coefficients à diminuer et, dans certains cas, à devenir nuls. Ce compromis fait en sorte que le modèle conserve les variables les plus importantes et en élimine d’autres. Le modèle ainsi obtenu est plus simple, plus facile à comprendre et moins enclin au surajustement.

Même dans les cas où les données comportent peu de variables, l’intégration d’interactions entre les variables dans le modèle peut conduire à l’existence de centaines, voire de milliers de variables uniques en interaction. La régression LASSO gère bien les interactions entre les variables prédictives, y compris le traitement de la colinéarité.

Pour réduire davantage le nombre de variables dans le modèle, on peut délibérément simplifier la régression LASSO en utilisant un lambda plus grand que celui que suggère la validation croisée, ce qui peut être souhaitable dans certains cas.

Considération des hypothèses existantes

En utilisant comme point de départ une table de mortalité existante, les modèles LASSO peuvent intégrer des hypothèses existantes. L’utilisation d’une valeur lambda, établie par validation croisée, produit un modèle qui met en balance les hypothèses existantes et les données. Ce modèle s’ajuste au plus près des données statistiques, lorsqu’elles sont suffisamment nombreuses, et au plus près des hypothèses existantes, lorsque les données statistiques sont peu nombreuses.

Interprétabilité

En plus d’avoir moins de coefficients, la régression LASSO produit des résultats sous une forme semblable à celle des MLG. Cette cohérence est avantageuse pour les actuaires qui connaissent déjà bien les MLG. En fournissant une formule interprétable pour générer des prédictions, la régression LASSO permet aux spécialistes de bien comprendre les principaux facteurs qui sous-tendent les prédictions du modèle, évitant ainsi la complexité des « modèles en boîte noire ».

En résumé

La régression LASSO combine les avantages des méthodes avancées d’apprentissage automatique et la simplicité des MLG. Elle permet de sélectionner efficacement des variables parmi une multitude de possibilités, tout en considérant les hypothèses existantes. Le terme de pénalité fait en sorte que seuls les coefficients pertinents sont inclus pour les variables ayant suffisamment de données à l’appui.

Pour l’essentiel, disons que la régression LASSO pousse à l’utilisation de modèles simples dans lesquels seules les variables les plus importantes contribuent de façon significative aux résultats. Ces modèles ont des coefficients que les actuaires peuvent facilement interpréter et utiliser pour établir des hypothèses.

Cet article présente l’opinion de ses auteurs et ne constitue pas un énoncé officiel de l’ICA.

Ouvrage de référence

TIBSHIRANI, Robert. « Regression Shrinkage and Selection via the Lasso », Journal of the Royal Statistical Society,série B (méthodologique),1996,vol. 58, no 1, p. 267-288.